Growth-rate measurement with type Ia supernovae within the ZTF photometric survey

Bastien Carreres

Image credits: ZTF.Caltech

Outline

  • Introduction:

    • The $\Lambda$CDM standard model

    • Modified gravity

  • Growth rate of structure

    • What is the growth rate of structure?

    • How to measure it?

  • Type Ia supernovae

    • What are they?

    • The Zwicky Transient Facility

  • The growth-rate analysis pipeline

    • Simulation

    • Analysis

  • Results

    • The sample bias

    • ZTF 6-years forecast

    • How to improve the measurement?

  • Other projects

    • Systematic effect on $H_0$ due to velocities

    • What's next?

  • Conclusion

The standard cosmological model: General Relativity + $\Lambda$CDM



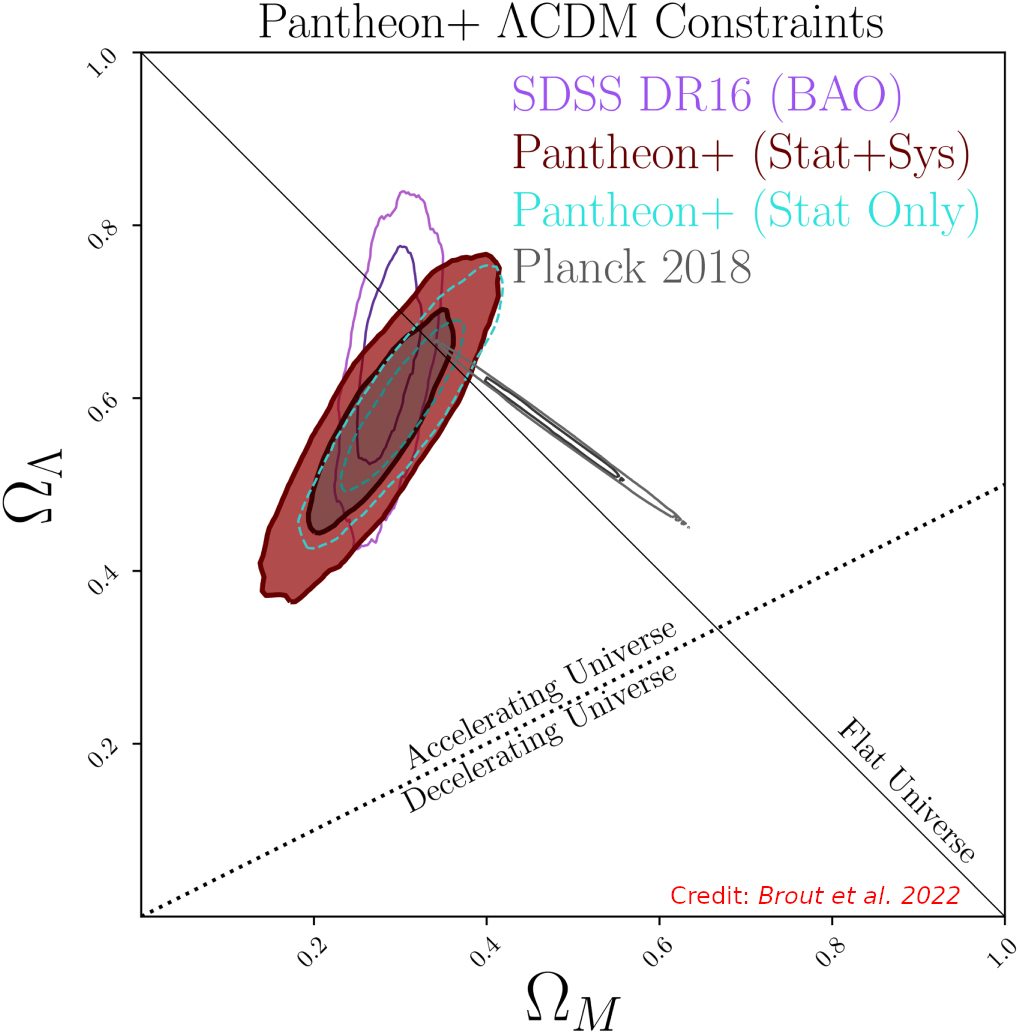
What is dark energy? Is there an alternative to $\Lambda$?

Modified gravity

Many models propose to explain accelerated expansion using new laws for gravity:

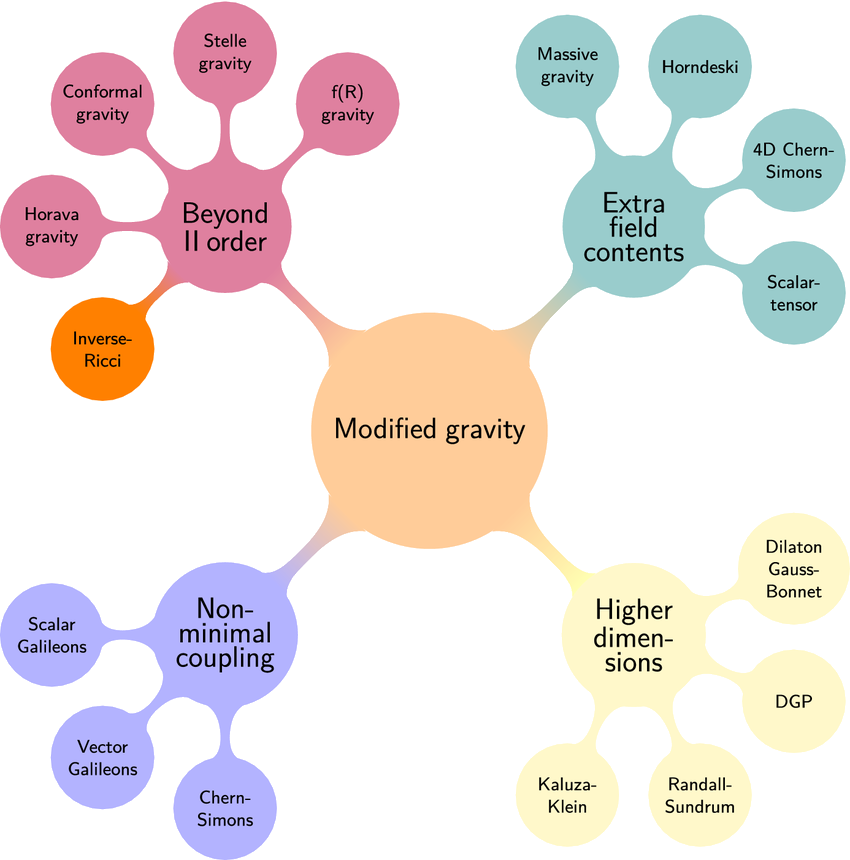
Changing gravity will affect structures formation

Image credits: arXiv:2204.06533

Outline

  • Introduction:

    • The $\Lambda$CDM standard model

    • Alternatives to $\Lambda$

  • Growth rate of structure

    • What is the growth rate of structures?

    • How to measure it?

  • Type Ia supernovae

    • What are they?

    • The Zwicky Transient Facility

  • The growth-rate analysis pipeline

    • Simulation

    • Analysis

  • Results

    • The sample bias

    • ZTF 6-years forecast

    • How to improve the measurement?

  • Other works

    • Systematic effect on $H_0$ due to velocities

    • What's next?

  • Conclusion

\(f\sigma_8\) as a probe for general relativity

Structure evolution:
Dark energy vs Gravity


Density contrast: $\delta(\mathbf{x}) = \frac{\rho(\mathbf{x})}{\bar{\rho}} - 1$


$\sigma_8$:
RMS of fluctuation over sphere of
8 Mpc.$h^{-1}$ radius

$\delta(\mathbf{x}) = \sigma_8 \tilde{\delta}(\mathbf{x})$

Velocities are linked to density through the continuity equation:

$\nabla.v(\mathbf{x}) \propto f\sigma_8 \tilde{\delta}(\mathbf{x})$

where $f \equiv$ growth rate

General Relativity + $\Lambda$CDM:
$f \simeq \Omega_m^\gamma$ with $\gamma \simeq 0.55$

Image credits: Illustris TNG

How to measure $f\sigma_8$ ?

Velocities as probes of $f\sigma_8$:
$\nabla.v \propto f\sigma_8$

Doppler effect on redshift:
$1 + z_\mathrm{obs} = \left(1 + z_\mathrm{cos}\right)\left(1 + z_p\right)$
$z_p \simeq \frac{v_p}{c}$, $v_p$ is the line-of-sight velocity

$v_p \sim 300 \ \mathrm{km}.\mathrm{s}^{-1}$ and $z_p \sim 0.001$


Direct velocity tracers
Data: redshifts + distances
Galaxies Tully-Fisher and Fundamental Plane: $\sigma_D/D \sim 20\%$
Type Ia supernovae: $\sigma_D/D \sim 7 \%$

Galaxies: Tully-Fisher & Fundamental plane relation

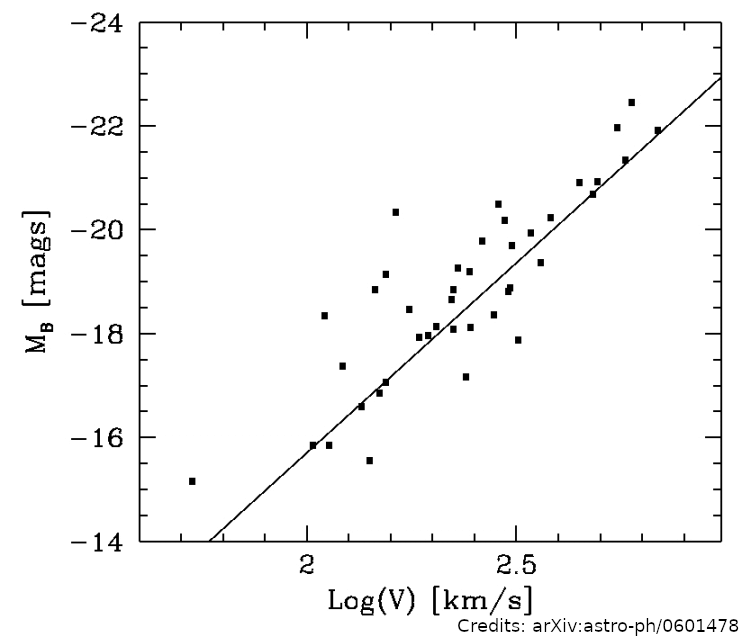
Image credits: Illustris TNG

Outline

  • Introduction:

    • The $\Lambda$CDM standard model

    • Alternatives to $\Lambda$

  • Growth rate of structure

    • What is the growth rate of structures?

    • How to measure it?

  • Type Ia supernovae

    • SNe Ia for cosmology

    • The Zwicky Transient Facility

  • The growth-rate analysis pipeline

    • Simulation

    • Analysis

  • Results

    • The sample bias

    • ZTF 6-years forecast

    • How to improve the measurement?

  • Other works

    • Systematic effect on $H_0$ due to velocities

    • What's next?

  • Conclusion

Type Ia supernovae (SNe Ia): powerful probes for cosmology

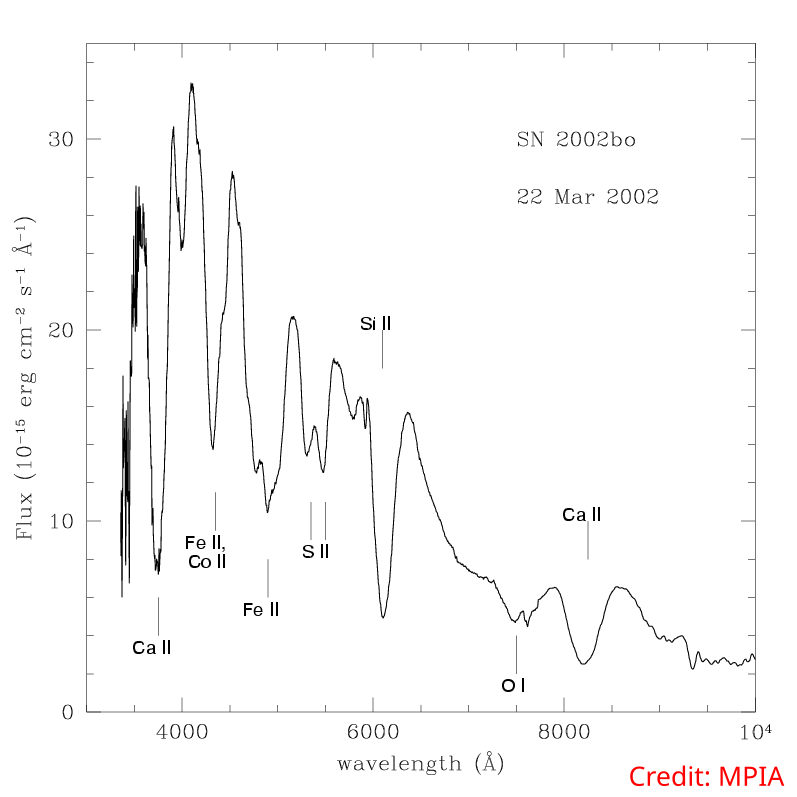
Distance modulus: $\mu = m_B - M_B \propto 5\log(d_L)$

SNe Ia: a few words about standardization

SNe Ia are not perfectly standard !!!

Correlation of peak magnitude with stretch, color and host galaxies exists

Tripp relation: $m_B^\mathrm{std} = m_B + \alpha x_1 - \beta c$

After standardization $\sigma_M \sim 0.12$

How to get $m_B$, $x_1$ and $c$?

Collect data

Adjust lightcurve with SALT2 (SED model for SNe Ia)






The Zwicky Transient Facility survey

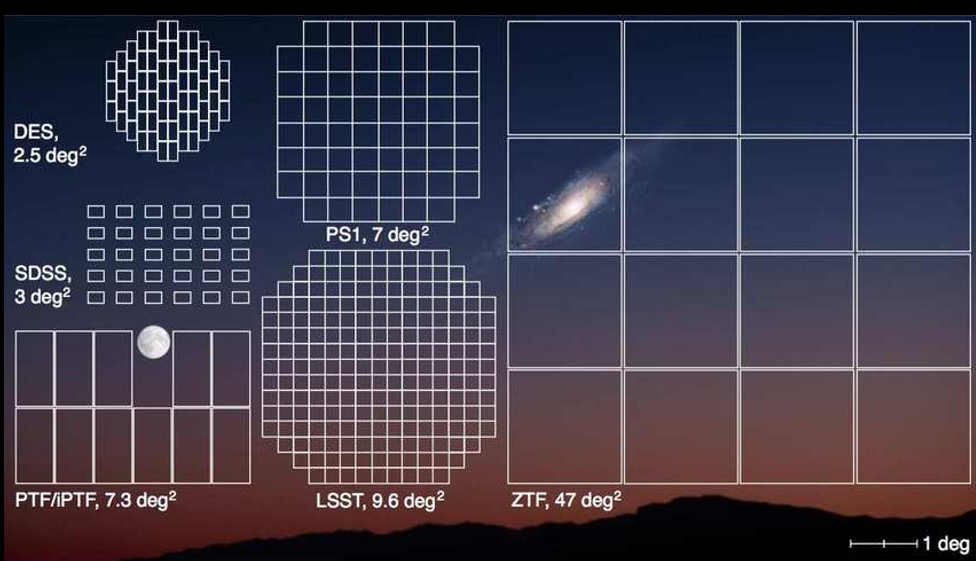
The ZTF survey:

  • Photometric telescope observing 3/4 of the sky every $\sim 2$ nights in 3 bands

  • Spectroscopic telescope measuring transient spectra

$\sim 8000$ classified supernovae
More than 3000 SNe Ia at low redshift $z < 0.1$

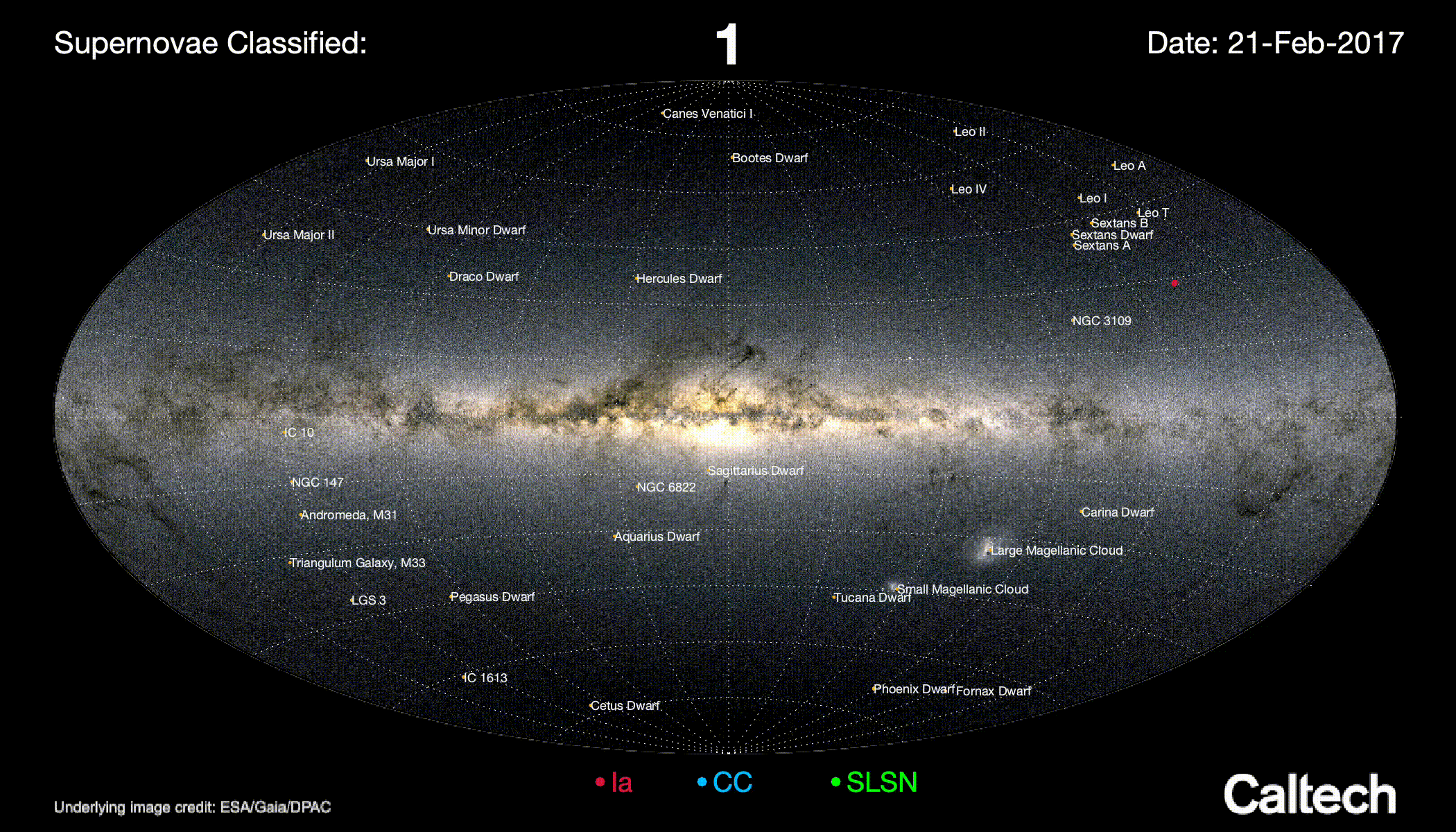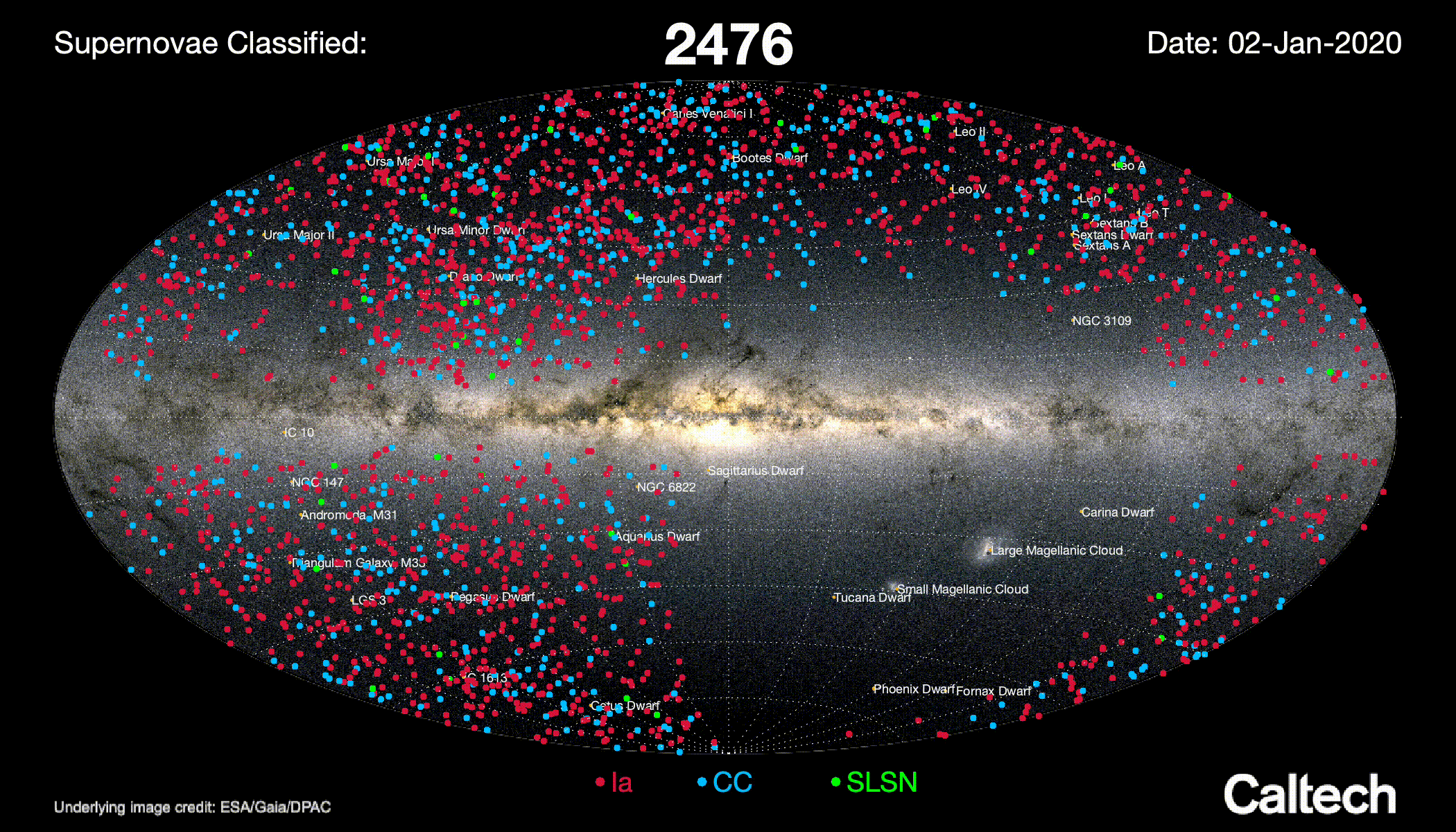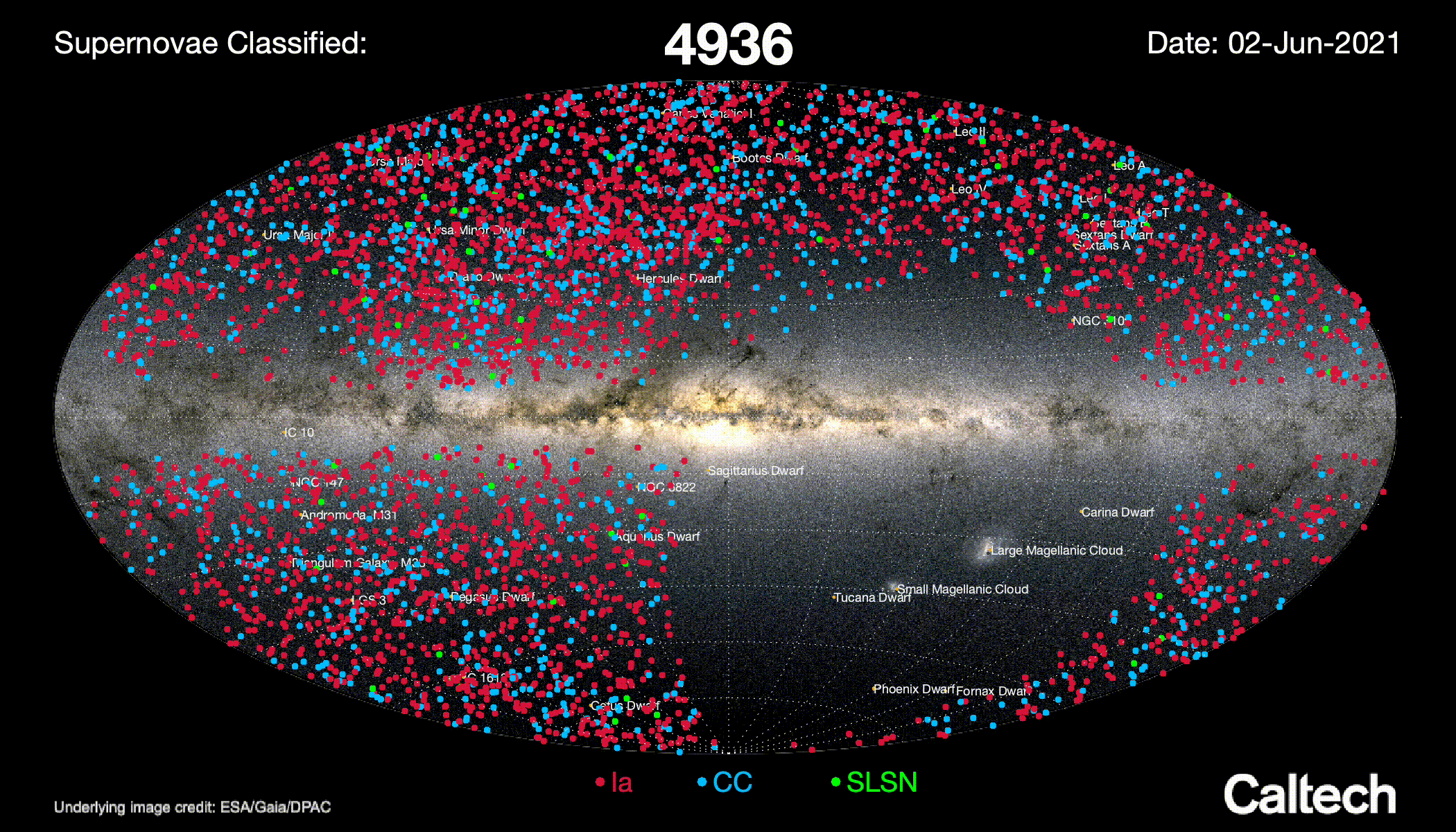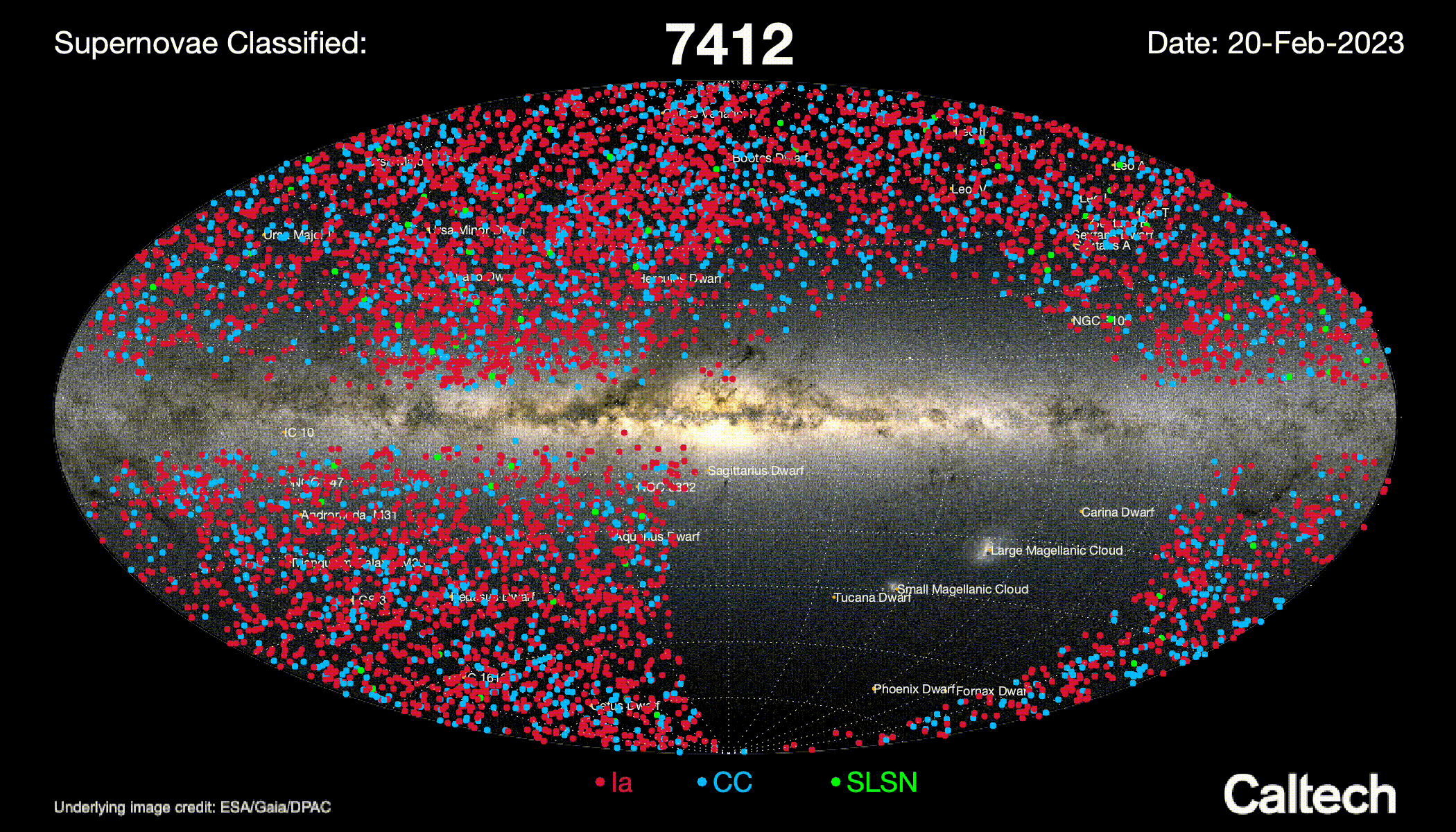
Image credits: ZTF.Caltech

Outline

  • Introduction:

    • The $\Lambda$CDM standard model

    • Alternatives to $\Lambda$

  • Growth rate of structure

    • What is the growth rate of structure?

    • How to measure it?

  • Type Ia supernovae

    • SNe Ia for cosmology

    • The Zwicky Transient Facility

  • The growth-rate analysis pipeline

    • Simulation

    • Analysis

  • Results

    • The sample bias

    • ZTF 6-years forecast

    • How to improve the measurement?

  • Other works

    • Systematic effect on $H_0$ due to velocities

    • What's next?

  • Conclusion

$f\sigma_8$ with SNe Ia peculiar velocities: the simulation and analysis pipeline

Simulation: the N-Body simulation

OuterRim (Heitmann et al. 2019)




WMAP cosmology, $f\sigma_8 = 0.382$



(3 Gpc.$h^{-1}$)$^3$ box of dark matter halos at $z=0$
$\Rightarrow$ 27 ZTF realisations up to $z\sim 0.17$

Simulation: SN Ia model



$1 + {\color{#96F1FD}z_\mathrm{obs}} = (1 + {\color{#96F1FD}z_\mathrm{cos}}) (1 + {\color{#96F1FD}z_\mathrm{p}})$


$m_{B,i} = {\color{#E78A0D}M_B} - {\color{#E78A0D}\alpha x_{1, i}} + {\color{#E78A0D}\beta c_i }+ {\color{#E78A0D}\sigma_{\mathrm{int}, i}} + \mu({\color{#96F1FD}z_{\mathrm{cos},i}}) + 10\log(1 + {\color{#96F1FD}z_{p,i}})$

Simulation: survey parameters

I have worked in ZTF simulation working group to construct ZTF simulation input files


Simulation: $\texttt{SNSim}$ and lightcurves

Noise is computed as

$\sigma_F = \sqrt{F + \sigma_\mathrm{sky}^2 + \sigma_\mathrm{ZP}^2}$

Simulation: applying spectroscopic identification selection function

Detection: 2 points with SNR $>$ 5

Spectroscopic efficiency from Perley et al. 2019

$\langle N_\mathrm{SN} \rangle\sim 4300$

$f\sigma_8$ with SNe Ia peculiar velocities: the simulation and analysis pipeline

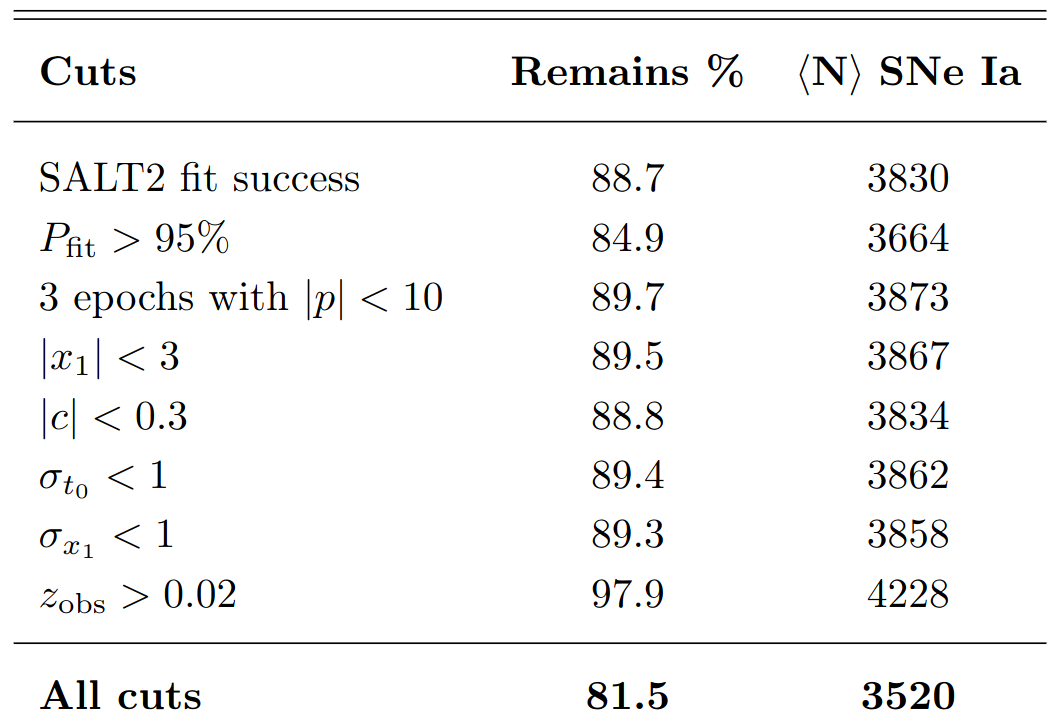
Analysis: lightcurves fit and cosmological cut

After SALT2 fit, we apply quality cuts:

Analysis: velocities from Hubble diagram residuals

Standard candles

Standard candles + velocities

Standard candles + velocities + noise

The velocity estimator:
$$\hat{v} = -\frac{\ln(10)c}{5}\left(\frac{(1+z)c}{H(z)r(z)} - 1\right)^{-1}\Delta\mu$$


The velocity estimator error:
$$\sigma_\hat{v} = -\frac{\ln(10)c}{5}\left(\frac{(1+z)c}{H(z)r(z)} - 1\right)^{-1}\sigma_\mu$$

Analysis: the Maximum-Likelihood method

Method used with galaxy data in Abate et al. 2010, Johnson et al. 2014 and Howlett et al. 2017

The correlation function depends on the Power Spectrum

$\langle v(\mathbf{x}_i)v(\mathbf{x}_j)\rangle \propto (f\sigma_8)^2 \int dk \tilde{P}(k) W^{(v)}(k; \mathbf{x}_i, \mathbf{x}_j)$

It gives us a $f\sigma_8$ dependent model for our covariance matrix!
$C_{ij}^{vv}(f\sigma_8) = \langle v(\mathbf{x}_i)v(\mathbf{x}_j)\rangle$

Two non-linear models of power spectra:


  • One based on N-body simulaton fit from Bel et al. 2019

  • One based on PT beyond order one from Taruya et al. 2012



Effect of redshift space distorsions taken into account with damping function $D_u(\sigma_u)$ (Koda et al. 2014)

Analysis: the Maximum-Likelihood method

Free parameters of the likelihood:

Growth-rate related parameters:

${\color{yellow} \mathbf{p} = \left\{f\sigma_8, \sigma_u, \sigma_v \right\}}$, $\sigma_u \equiv$ RSD, $\sigma_v\equiv$ non-linearities

The likelihood:

$\mathcal{L}({\color{yellow}\mathbf{p}}) \propto |C({\color{yellow}\mathbf{p}})|^{-\frac{1}{2}} \times\exp\left[-\frac{1}{2}\mathbf{v}^TC({\color{yellow}\mathbf{p}})^{-1}\mathbf{v}\right]$


The covariance:

$C_{ij}({\color{yellow}\mathbf{p}}) = C^{vv}_{ij}({\color{yellow}f\sigma_8}, {\color{yellow}\sigma_u}) + {\color{yellow}\sigma_v}^2 \delta^K_{ij} + \sigma_\hat{v}^2 \delta^K_{ij}$

$C^{vv}_{ij}({\color{yellow}f\sigma_8}, {\color{yellow}\sigma_u}) = \langle v(\mathbf{x}_i)v(\mathbf{x}_j)\rangle \propto ({\color{yellow}f\sigma_8})^2 \int dk P(k) W(k) D_u^2(k; {\color{yellow}\sigma_u}) $

Outline

  • Introduction:

    • The $\Lambda$CDM standard model

    • Alternatives to $\Lambda$

  • Growth rate of structure

    • What is the growth rate of structures?

    • How to measure it?

  • Type Ia supernovae

    • SNe Ia for cosmology

    • The Zwicky Transient Facility

  • The growth-rate analysis pipeline

    • Simulation

    • Analysis

  • Results

    • The sample bias

    • ZTF 6-years forecast

    • How to improve the measurement?

  • Other works

    • Systematic effect on $H_0$ due to velocities

    • What's next?

  • Conclusion

Results: the selection bias (Carreres et al. 2023)

Bias on HD residuals

Bias on velocity estimates

$$\hat{v} = -\frac{\ln(10)c}{5}\left(\frac{(1+z)c}{H(z)r(z)} - 1\right)^{-1}\Delta\mu$$




Only the estimated velocities are biased !!!

Bias on $f\sigma_8$

Results: forecast for a ZTF 6-years complete sample (Carreres et al. 2023)

$z \lt 0.06 \Rightarrow \langle N_\mathrm{SN} \rangle \simeq 1600 \sim$ half of the sample

Analysis: joint fit

Free parameters:

Growth-rate related parameters: ${\color{yellow} \mathbf{p} = \left\{f\sigma_8, \sigma_u, \sigma_v \right\}}$

SNe Ia Hubble diagram parameters: ${\color{orange} \mathbf{p}_\mathrm{HD} = \left\{\alpha, \beta, M_B, \sigma_M \right\}}$


Data vector

HD residuals: $\Delta \mu({\color{orange} \mathbf{p}_\mathrm{HD}}) = m_B + {\color{orange} \alpha} x_1 - {\color{orange} \beta} c - {\color{orange} M_0} - \mu_\mathrm{model}(z)$

$\hat{v} \rightarrow \hat{v}({\color{orange} \mathbf{p}_\mathrm{HD}})= -\frac{\ln(10)c}{5}\left(\frac{(1+z)c}{H(z)r(z)} - 1\right)^{-1}\Delta\mu({\color{orange} \mathbf{p}_\mathrm{HD}})$


Covariance

$\sigma_\hat{v} \rightarrow \sigma_\hat{v}({\color{orange} \mathbf{p}_\mathrm{HD}})= \frac{\ln(10)c}{5}\left(\frac{(1+z)c}{H(z)r(z)} - 1\right)^{-1}\sigma_\mu({\color{orange} \mathbf{p}_\mathrm{HD}})$

Results: forecast for a ZTF 6-years complete sample (Carreres et al. 2023)

$\langle N_\mathrm{SN} \rangle \simeq 1600 \sim$ half of the sample

Results: comparison with existing measurements (Carreres et al. 2023)


With ~1600 SNe Ia, ZTF is at the same precision level as existing measurements with several thousands of galaxies

Results: could a bias correction improve the constraint? (Carreres et al. 2023)

Simulate a perfect correction of the bias: $v_{\mathrm{debias}, i} \sim \mathcal{N}(v_\mathrm{true}, \sigma_{\hat{v}, i})$

How to improve the measurement?

  • Bias correction of the velocity estimates ?

    Does not improve strongly the constraint on $f\sigma_8$



  • Use photo-typing to increase the redshift limit



  • Velocity $\times$ density measurements (e.g. ZTF + DESI)

Future surveys

Forecast credits: DESI arxiv:1611.00036, LSST arxiv:1708.08236, EUCLID arXiv:1606.00180

Outline

  • Introduction:

    • The $\Lambda$CDM standard model

    • Alternatives to $\Lambda$

  • Growth rate of structure

    • What is the growth rate of structures?

    • How to measure it?

  • Type Ia supernovae

    • SNe Ia for cosmology

    • The Zwicky Transient Facility

  • The growth-rate analysis pipeline

    • Simulation

    • Analysis

  • Results

    • The sample bias

    • ZTF 6-years forecast

    • How to improve the measurement?

  • Other works

    • Systematic effect on $H_0$ due to velocities

    • What's next?

  • Conclusion

Systematic effect on $H_0$ due to velocities (paper in prep)

Hubble Diagram fit



$\Delta\mu = m_B + \alpha x_1 - \beta c - M_0 - \mu_\mathrm{model}(z)$

where $M_0$ is degenerate with $H_0$




Velocity error term:

$\sigma_{\mu-z} = \frac{5}{\ln 10} \frac{\sigma_v}{z}$

with $c\sigma_v \simeq 250$ km/s

We use our 27 mocks from $\texttt{SNSim}$ that contain correlated velocities to evaluate velocities effect in Hubble diagram fit

Systematic effect on $H_0$ due to velocities (paper in prep)


Velocities not taken into account

Diagonal term for velocity errors

Full covariance matrix for velocities

Preliminary results: using full covariance matrix multiplies by ~4 the error on $M_0$ on simulations. First test on ZTF DR2 data gives an error multiplied by ~2.

What's next?

  • Improve the simulation:

    • Include more realistic noise, correlation with host properties, color-dependant scattering


  • Evaluate the photometric sample:

    Work started with D. Rosselli in a Vera Rubin/DESC project


  • Generalisation to velocity-density covariance + improvements of model computation:

    Work started with C. Ravoux: development of the $\texttt{flip}$ public package


  • Application of the $f\sigma_8$ analysis to ZTF data

Conclusion

  • I developed a simulation of supernovae observations including realistic velocities from N-body simulations

  • I used real observation conditions to generate ZTF survey realizations

  • I developed a full analysis pipeline to measure $f\sigma_8$ from SNe Ia

  • The spectroscopic selection causes a bias on velocity estimations above $z\sim 0.06$

  • We forecast that we will have a ~19% precision on a $f\sigma_8$ measurement with a 6-year ZTF SNe Ia spectro-identified sample with $z\lt 0.06$

  • Improvements are expected from future work on photometric typing analysis and combination with density measurements

Backup slides

$f\sigma_8$ as a function of $z_\mathrm{max}$

Velocity estimators biases

$\hat{v}_1 = -\frac{\ln(10)c}{5}\left(\frac{(1+z)c}{H(z)r(z)} - 1\right)^{-1}\Delta\mu$

$\hat{v}_2 = -\frac{\ln(10)}{5}\frac{H(z)r(z)}{(1+z)}\Delta\mu$

$\hat{v}_3 = -\frac{\ln(10)c}{5}\left(\frac{1+z}{z} - 1\right)^{-1}\Delta\mu$

$\hat{v}_4 = -\frac{\ln(10)c}{5}\frac{z}{1+z}\Delta\mu$

Gaussian prior on $\sigma_u$

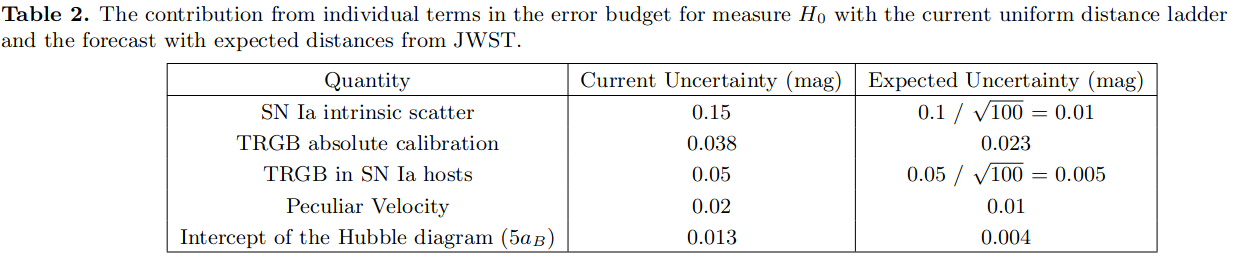
ZTF $H_0$ budget erro(Dhawan et al. 2021)